Основные состояния
1. Основные состояния чётно-чётных ядер имеют спин/чётность 0+.
2. Значение спина считается установленным точно, если оно получено при помощи таких методов как резонанс на атомных пучках, парамагнитный резонанс, спин-электронный "спин-эхо" резонанс и оптическая спектроскопия.
Гамма-переходы
3. Согласие измеренного значения коэффициента одиночной конверсии с теоретическим значением для мультипольности, которое хорошо отделяется от значения для любой другой мультипольности, определяет мультипольность перехода.
4. Во всех других случаях, если нет других оснований для назначения мультипольности, для установления мультипольностей перехода и коэффициента смешивания необходимо согласие двух или более измеренных коэффициентов конверсии или их отношений с теоретическими значениями.
5. Так как E0-переходы могут идти только путём конверсии или образованием пары, то, если наблюдались фотоны, чистые E0 исключаются.
6. Рекомендуемые верхние пределы на силы
гамма-переходов
![]()
![]() /
/![]() w,
w,![]() w
w
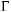
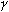 /
/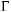 w (верхний предел)
---------------------------------
Переход* A=6-44a$ A=45-150b,c A>150d
E1 (IV) 0,3# 0,01 0,01
E2 (IS)e 100 300 1000
E3 100 100 100
E4 100 100@
M1 (IV) 10 3 2
M2 (IV) 3 1 1
M3 (IV) 10 10 10
M4 30 10
* 'IV' и 'IS' означают изовектор и изоскаляр
@
w (верхний предел)
---------------------------------
Переход* A=6-44a$ A=45-150b,c A>150d
E1 (IV) 0,3# 0,01 0,01
E2 (IS)e 100 300 1000
E3 100 100 100
E4 100 100@
M1 (IV) 10 3 2
M2 (IV) 3 1 1
M3 (IV) 10 10 10
M4 30 10
* 'IV' и 'IS' означают изовектор и изоскаляр
@ 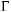
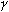 /
/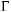 w(верхний предел)=30 для A=90-150
#
w(верхний предел)=30 для A=90-150
# 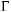
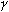 /
/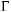 w(верхний предел)=0,1 для A=21-44
$
w(верхний предел)=0,1 для A=21-44
$ 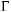
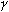 /
/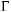 w(верхний предел)=0,003 для E1 (IS),
10 - для E2 (IV), 0,03 - для M1 (IS), 0,1 - для M2 (IS)
a Из 1979En05
b Из 1979En04
c Из 1981En06
d Выведено M. J. Martyn из ENSDF
e В супер-деформированных полосах E2-переходы могут иметь
w(верхний предел)=0,003 для E1 (IS),
10 - для E2 (IV), 0,03 - для M1 (IS), 0,1 - для M2 (IS)
a Из 1979En05
b Из 1979En04
c Из 1981En06
d Выведено M. J. Martyn из ENSDF
e В супер-деформированных полосах E2-переходы могут иметь 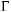
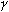 /
/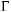 w>1000.
w>1000.
Бета-переходы (см. 1973Ra10)
7. Если log ft < 5,9,
то переходы являются разрешенными:
![]() J=0
J=0![]()
![]() =no
=no![]() T=0)
T=0)![]() T=1)
T=1)
8. Если
log f1ut < 8,5
(log f't < 7,4), то
![]() J=0,1;
J=0,1;![]()
![]() =yes или no.
=yes или no.
9. Если
log ft < 11,0, то
![]() J=0,1;
J=0,1;![]()
![]() =yes или no
=yes или no![]() J=2;
J=2;![]()
![]() =yes.
=yes.
10. Если
log ft < 12,8, то
![]() J=0,1,2;
J=0,1,2;![]()
![]() =yes или no.
=yes или no.
11. Если
![]() 8,5
8,5![]() 7.4)
7.4)![]() J=2,
J=2,![]()
![]() =yes).
=yes).
Смотрите раздел
"Вероятность бета-распада".
Отметим, что
log f1ut =
log f't + 1,079.
Замечание: для нуклидов с заполненной оболочкой, или очень близких к заполненным оболочкам, значения могут быть меньше. Например, в районе около Z=82, верхний предел 5,9, приведённый в пункте 7, будет приблизительно 5,1.
![]() -корреляция направлений
-корреляция направлений
![]()
12. Если экспериментальные значения
коэффициентов ![]() -корреляций
направлений составляют
-корреляций
направлений составляют
![]() +0,36
+0,36![]() +1,1,
+1,1,![]() 2
2![]() 0.
0.
13. Результаты
![]() (
(![]() )
)
![]() -корреляция направлений
-корреляция направлений
![]()
14. Если
![]() ,
то переход неразрешённый. Обратное неверно.
,
то переход неразрешённый. Обратное неверно.
15. Если
![]() )
)![]() 0,
0,
16. Если
![]() )=0,
)=0,
![]() -поляризационная корреляция
-поляризационная корреляция
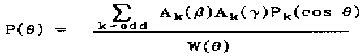
17. Для разрешённых переходов
| A1( | ||
| A1( | ||
| A1( | ||
| A1( | ||
| A1( | ||
| A1( |
18. Если
![]() )
)![]() 0,
0,![]() -переход
-переход
Угловое распределение ![]()
19. В угловом распределении гамма-излучения из
разрядки состояний, заселённых в реакциях с большим спином (с типовыми значениями
![]() /J=0.3,
/J=0.3,![]() - параметр заселения магнитного подсостояния):
- параметр заселения магнитного подсостояния):
![]() DCO отношение
DCO отношение
В угловом распределении (DCO)
гамма-излучения из разрядки состояний, заселённых
в реакциях с большим спином (с типичным значением
![]() /J=0,3,
/J=0,3,![]() - параметр заселения магнитного подсостояния).
- параметр заселения магнитного подсостояния).
20. Для
![]() J=2,
J=2,
21. Для
![]() J=1;
J=1;
Реакции
22. Кулоновское возбуждение при низких энергиях в основном приводит к E2-возбуждению.
23. Кулоновское возбуждение определяет
![]() ,
,
24. Спин компаунд-состояния, полученного захватом теплового нейтрона, равен спину исходного ядра плюс или минус 1/2.
25. Первичное гамма-излучение из реакции захвата нейтрона может быть E1, M1, E2 или M1+E2.
26. Если угловое распределение в реакции однонуклонной передачи может быть описано одним значением L, то спин конечного состояния Jf может быть выражен через спин исходного состояния Ji (векторно)
Jf = Ji + L + 1/2
с изменением чётности, если значение L нечётно.
27. Если из векторного анализа однонуклонной реакции передачи следует явное преобладание либо J=L+1/2, либо J=L-1/2 и, если L - известно, то считается, что значение J установлено.
28. В общем случае для состояний, заселяемых в реакциях с большим значением спина, спины увеличиваются с увеличением энергии возбуждения. Это является результатом того факта, что эти реакции имеют тенденцию к заселению ираст-состояний или близких к ним.
29. Если угловое распределение может быть описано
единственным значением L, то
![]()
![]()
![]() f
f![]() i=(-1)L,
i=(-1)L,
30. В реакциях с
![]() =0+
=0+
31. В реакциях с поляризованными частицами при
![]() =1
=1![]() =0+
=0+
Области сильной ядерной деформации
Систематическое проявление структуры
ротационных полос в сильно-деформированных ядрах может оказать значительную
помощь в приписывании
![]() ,
,![]()
32. Соображения, основанные на энергиях уровней. Если группирование состояний не является слишком сильным, то энергии наиболее низколежащих членов полосы могут быть выражены относительно простым соотношением (см. 1971Bu16 и ссылки в ней):
| |
(1) |
где X=J(J+1)-K2
Инерциальный параметр, A, проявляет систематическое поведение в различных областях сильнодеформированных ядер, что может быть полезно для приписания уровней ротационным полосам. В некоторых примерах (например, сильное Кориолисово связывание), когда значения A могут сильно отклоняться от систематического поведения, такие наблюдения могут быть полезны сами по себе, так как могут позволить установить наличие таких эффектов и, следовательно, помочь найти основания для приписани я ядерной конфигурации.
В случае полос с K=1/2, параметр развязывания, который характерен для каждой такой полосы, даётся отношением A1/A в формуле (1). Установление значения параметра развязывания предполагаемой полосы может оказаться полезным при назначении ей ядерной конфигурации, и наоборот.
33. Разрешённые незаторможенные бета-переходы.
В этой области бета-переходы, имеющие значения
log ft < 5,0, классифицируются
как "разрешённые незаторможенные" (au). Такие переходы
происходят между одночастичными орбиталями, имеющими одни и те же
асимптотические квантовые числа. В области "редких земель"
![]() N
N![]() 112,
112,![]() Z
Z![]() 76),
76),
34. Кулоновское возбуждение.
Если обнаружена последовательность
уровней "ротационно-подобного" характера по энергиям, возбуждаемая с повышенной
вероятностью, то это является основанием того, что эта последовательность
(по крайней мере, несколько наинизших, до первого "бэкбендинга")
образует ротационную полосу на базе основного состояния.
Если вероятности E2-переходов являются большими (десятки
единиц Вейскопфа или более) и сравнимыми друг с другом, то имеется
основание рассматривать их как имеющих структуру полосы и приписать
последовательные значения
![]() ,
,
35. Альфа-распад.
Наблюдение "благоприятного" (не замедленного - ред.)
альфа-перехода (HF<4) указывает на то, что оба вовлечённых состояния
имеют одинаковую ядерную конфигурацию. Если последовательность уровней,
связанных с заселяемым уровнем этим "благоприятным" переходом,
имеет "ротационно-подобный" характер и эти уровни имеют значения HF, которые
изменяются в соответствии с установленной тенденцией ротационных полос
(1972El21), то эта последовательность может рассматриваться как образующая
ротационную полосу, и её ядерная конфигурация та же, что и в распадающемся
состоянии. Если значение
![]()
36. Реакции однонуклонной передачи (инициированные лёгкими ядрами).
Для реакций однонуклонной передачи, инициированных лёгкими ядрами
(4He и более лёгкими), характерное поведение сечения
взаимодействия среди членов ротационной полосы ("отпечаток") может
использоваться для назначения набора уровней ротационной полосе
основанной на данной Нильссоновской конфигурации с соответствующими
![]() ,
,
Высокоспиновые состояния
При распаде высокоспиновых состояний, обычно появляющихся при реакциях на тяжёлых ионах или при образовании высоковозбуждённых состояний в реакциях деления или кулоновского возбуждения, мультипольности разряжающих состояний гамма-квантов и относительные спины и чётности уровней обычно определяются из угловых распределений, угловых корреляций (отношений DCO), линейных поляризаций и коэффициентов внутренней конверсии. Вдобавок, относительное расположение энергий уровней и увеличение гамма-интенсивностей с уменьшением энергии возбуждения, является важной информацией.
37. Для сильнодеформированных ядер, когда
наблюдается регулярная последовательность переходов с
![]() J=2
J=2![]() J=2
J=2
38. Для ядер, близких к сферическим,
где наблюдаются переходы с регулярной последовательностью
![]() J=1
J=1![]() J=1
J=1
39. В случае отсутствия данных по угловым
распределениям/корреляциям
регулярная последовательность переходов в каскаде может быть приписана
общей структуре или полосе, если:
а) низколежащие уровни этой структуры имеют хорошо установленные значения
спина и чётности и
б) существуют серьёзные основания считать, что при больших значениях энергий
и спинов, полоса не меняет внутреннюю структуру по причине пересечения
полос или других возмущений.
Альфа-распад
40. Фактор замедления для альфа-переходов
из основного состояния чётно-чётных
ядер в основное состояние дочерних ядер по определению равен 1. Для ядер с
нечётным A или нечётно-нечётных ядер значение фактора замедления
![]() 4
4
41. Для альфа-распада между двумя
состояниями, одно из которых имеет J=0, изменение чётности даётся выражением
![]()
![]() =(-1)
=(-1)![]() J.
J.
Протонная радиоактивность
42. Спин и чётность уровня, проявляющего
протонную радиоактивность и принадлежащего к околосферическому Z-чётному,
N-нечётному ядру, могут быть приняты равными величинам
![]()
а) переход идёт на основное состояние дочернего ядра;
б) значения
![]()
в) вычисленное значение времени жизни
относительно протонного распада для этих значений
![]()
г) вычисленное значение времени жизни
относительно протонного распада для других физически возможных значений
![]()
1. В тех случаях, когда гамма-кванты одной мультипольности "группируются" в одном районе на графике зависимости времён жизни от энергии, как это справедливо для M4, другим гамма-квантам, чьи времена жизни попадают в этот район, можно приписать соответствующую мультипольность.
2. В тех случаях, когда "группировки" для двух мультипольностей, как, например, для M1 и E2, попадают в один район времён, то новым гамма-квантам, чьи времена жизни попадают в этот район, можно приписать любую из этих мультипольностей, или их смесь.
3. Всякий раз когда
![]() J
J![]() 2,
2,
Это утверждение основано на недостатке контрпримеров и наблюдении, что немногочисленные E2 гамма-кванты также медленны, как M3, немногочисленные M2 гамма-кванты также медленны, как E3, и так далее.
4. Спин и чётность родительского состояния может быть выведен из измеренных свойств их предполагаемого изобарно-аналогового резонанса, и наоборот.
5. Низколежащие состояния ядер с нечётным A имеют спины и чётности, следующие из оболочечной модели, за исключением областей деформированных ядер. Это утверждение более строго при поддержке значений силовой функции (C2S) в реакциях однонуклонной передачи.
Здесь признаётся, что некоторые выводы оболочечной модели более
сильны, чем другие. Например, оболочечная модель достаточно мягко отрицает,
что
![]()
6а. Для низко-лежащих состояний нечётно-нечётных сферических ядер может быть полезны правила Нордхейма (1950No10):
J = jp+jn, если jp=lpмогут быть полезны для получения спинов и чётностей основных состояний, при условии, что они подтверждаются какими-либо ещё основаниями.1/2 и jn=ln
1/2;
J = |jp-jn|, если jp=lp1/2 и jn=ln
1/2.
6б. Для возбуждённых состояний сильно-деформированных нечётно-нечётных ядер
могут быть полезны правила Галлахера-Можковского (1958Ga27) для вывода
относительных положений двух двухквазичастичных состояний, образуемых двумя
различными спариваниями составных квазичастиц, при условии, что они
подтверждаются ещё какими-либо основаниями. Так, для состояния, соответствующему
параллельному расположению
![]() =1)
=1)![]() =0)
=0)![]()
(В сильно-деформированных чётно-чётных ядрах можно ожидать обратную картину,
то есть, при
![]() =0
=0![]() =1.
=1.
7. Утверждения, подобные пунктам 5 и 6, основанные на других моделях.
8. Утверждения, основанные на интерполяции или экстраполяции тенденций, подмеченных в каких-либо районах ядер, таких как показано в 1971Bu16, 1972El21, 1977Ch27, 1990Ja11 и 1998Ja08 для районов "редких земель" и тяжёлых ядер.
9. Все утверждения, связанные с ненаблюдением ожидаемых переходов.
10. Правила, извлечённые из обзора 1972El21 по "неблагоприятным" альфа-переходам, могут использоваться для вывода конфигурации родительского или дочернего уровня, при условии, что конфигурация другого известна.
11. Для магнитных моментов крайняя редкость чистых одночастичных состояний и наблюдение больших отклонений от g-фактора свободного нуклона в ядрах означает, что сравнение между экспериментом и оценками из 'Шмидтовских ограничений' (основанных на таких чистых состояниях) не даёт основания для назначения спина и чётности. Магнитные моменты или g-факторы, тем не менее, могут дать некоторые основания для назначений где предсказания для возможных альтернатив, сделанных с использованием g-факторов, основанных на локальных систематиках измеренных моментов, сильно отличаются.
Для возбуждённых состояний 'коллективные' аспекты состояния часто дают существенный вклад в магнитный момент. Поправка g-фактора на этот вклад - это дело детальной теории и любые назначения, основанные на подразумеваемом g(коллективное)=Z/A должны рассматриваться с осторожностью.