CENTRE FOR PHOTONUCLEAR EXPERIMENTS DATA
NUCLEAR QUADRUPOLE DEFORMATIONS
Electronic Chart of Deformation gives to one possibility to obtain in comfortable form (analogous to that of well-known Charts of the Nuclides) numerical information for various nuclear deformation parameters (quadrupole moment Q and quadrupole deformation parameter b2) for ground states of many nuclei and contains the data from three sources:
- [1] S.Raman, C.W.Nestor, P.Tikkanen. Atomic Data and Nuclear Data Tables, 78, 1 (2001). - Transition Probability from the Ground to the First-Excited 2+ State of Even-Even Nuclides - reduced transition probability B(E2)↑ (0+ ® 2+) data;
- [2] N.J.Stone, Atomic Data and Nuclear Data Tables, 90 75(2005) - Table of data on nuclear magnetic dipole and electric quadrupole moments - quadrupole moment data;
- [3] B.S.Ishkhanov, V.N.Orlin. Yadernaya Fizika, 68, 1407 (2005) - - quadrupole deformation parametrs calculated in the frame of model essence of which is obtaining of equilibrium nucleus shape from the conditions of minimization of single-particle energies sum.
from its quadrupole moment.
Intrinsic quadrupole moment of evenly charged ellipsoid can be described by equation
where b is large, and a is small ellipsoid axises.
Since quadrupole deformation parameter δ (degree of nucleus shape difference from sphere) can be written as
where average mean-squared charge distribution radius is equal to
equation (1) would be the following
Hense, using experimental quadrupole moment values the nucleus quadrupole deformation parameter values δ could be calculated by the formula
Moment Q0 values were recalculated from static electric quadrupole moment Q values measured in laboratory system. It was supposed than near spherical nucleus shape vibrations amplitude is small in comparison to nucleus equilibrium deformation and therefore the equation
where I is spin of state studied - the member of rotational band based on nucleus ground state, K is I's projection on symmetry axis (the joint characteristics of all band members).
Value of <r2> was evaluated using the following expressions
which takes into account effects of light nuclei surface diffusion properties.
Parameters of radial Woods-Saxon potential form-factor
were obtained from the data on fast electrons scattering.
from the value of reduced transition probability B(E2) for (0+ ® 21+) transition.
Nucleus quadrupole deformation parameter was obtained using the following equation
where B(E2; 0+®21+) is reduced probability for Å2- transition from ground 0+ to first excited 2+1 state and R02 = (1.2 A1/3 sm)2.
Default the data from all information sources used are presented; if it is needed the data presentation of any type could be switch out using the buttons of panel displayed under the Chart.
The four scales are used in the Chart, the panel “Fast Search” is intended to mark the proton number Z and neutron number N for concrete nucleus looked for.
With the aim of simplifying of searching and identification of data for looked for nucleus (or nuclei group) the special colors are used (in a manner similar to that for traditional geographical maps) - brown (“mountains”) - for nuclei with positive deformation, blue (“oceans”) - negative, and green (“plains”) - for nuclei with unknown sign of deformation or with zero deformation.
5 color intensity degrees identify the parameter of deformation absolute values – more intensive color corresponds to larger value.
After the click on the looked for nucleus Chart element using the smallest Chart scale all quadrupole moment Q and quadrupole deformation parameter b2 values correspondent to marked before information source (sources) together with data for energy and spin-parity for correspondent nucleus levels are presented in the additional window.
NUCLEAR RADII DATA
NUCLEAR CHARGE RADII – 2008
Yu.Gangrsky and K.Marinova*)Joint Institute for Nuclear Research, 141 980 Dubna, Moscow region, Russia
*) e-mail: marinova@nrmail.jinr.ru
This table is a result of a combined analysis of two types of experimental data on nuclear charge radii. The first type yields data on rms charge radii R = <r2>1/2 from electron scattering experiments (el) and muonic atom spectra (mu) and the second - on ms charge radii changes δ<r2> from optical isotope shifts (OIS). The <r2> is root-mean-square radius. The combined treatment is applicable to those elements for which both types of data exist. Since the absolute radii R are known only for the stable isotopes, the extension of the neutron number far off stability is determined by the range of δ<r2> data. Thus, the table presents a new set of nuclear radii covering 59 elements from He to Cm (809 isotopes).
The least-squares method for the combined analysis described in detail in [Na94] remains unchanged. The updated values of nuclear charge radii in the present table differ from those in [Na94] due to changed input data on R and δ<r2>. The following should be noted:
- Now, the main source for the R values is the table of [An99]. The few exceptions are displayed in the reference list (see the comments below).
- In the most cases, original papers on optical isotope shifts instead of review papers are used and treated with the necessary precaution. In the procedure of extracting the nuclear parameter λ, the semiempirical approach using optical information was preferred. Experimental λ were converted in δ<r2> values using the corrections for the higher-order radial moments given by [Fr04]. References for the input data on δ<r2> are pointed out for each isotope in the table.
- Since 1994 many new optical data on radii changes have been published. In the present table more recent data, including early 2008, are taken into account.
Comments
- For nine elements (Ca, Kr, Sr, Zr, Mo, Sn, Sm, Gd, and Pb) the R-values in the table of [An99] are obtained taking into account the experimental results from optical isotope shifts, too. To ensure correct analysis of both type of experimental data, nonopical (el-mu) and optical (OIS), another sources of rms radii R have been used in these cases [An08, Wo81].
- For the radioactive elements Po, Rn, Fr, Ra and Cm there are no experimental R data. Reference radii R0 for an appropriated chosen isotope in the isotopic sequences of these elements are calculated by equation (22) of [An99] using the parameters of [An08].
Acknowledgment: The authors are indebted to I.Angeli for supplying additional information on rms charge radii R and for the helpful discussion.
REFERENCES
[An99] I.Angeli, Table of nuclear root mean square charge radii, INDC(HUN)-033, September 1999
(IAEA Nuclear Data Section, Vienna).
[An08] I.Angeli, private communication (2008), Kr, Sr, Zr, Mo, Sn, Sm, Gd, Pb, 202Po, 212Rn, 212Fr , 214Ra, 244Cm, Th, U, Pu.
[Fr04] G.Fricke, K.Heilig, Landolt-Bornstein: Num. Data and Funct. Relat. in Science and
Tech. New Series, Group I: Elem. Part., Nuclei and Atoms, v. 20 (2004).
[Na94] E.G.Nadjakov et al., At. Data Nucl. Data Tables 56 (1994) 133.
[Wo81] H.D.Wohlfahrt et al. Phys. Rev. C23 (1981) 533, Ca.
RECOMMENDED VALUES OF NUCLEAR CHARGE RADII - 2008"
Institute of Experimental Physics, University of Debrecen,
H-4010 Debrecen, Pf. 105.
E-mail: angeli@tigris.unideb.hu
The present table contains 865 rms nuclear charge radii. For absolute R values experimental data from electron scattering (e-), muonic atom X-rays (μ-), as well as Lamb shift (for the proton) were taken into account. For differences δR, in addition to e- and μ-, data from Ka isotope shifts (KIS) and optical isotope shifts (OIS) were used. Constraints between δR and R values were exploited wherever possible. Therefore, this table is not a simple compilation of individual measurements, but rather a more or less consistent set of R values.
The data sources and treatment has been described in detail in [An99] for the R values from e‑ and μ‑ methods, while in [An04] the treatment of differences δR is given. Here only the changes are briefly mentioned. New data: the reference list presents the sources of data, published or found since the previous table. Change in the evaluation: for the absolute R data from e‑ and μ‑ methods, the simpler and more transparent averaging formulae were used (EXCEL) instead of the lengthy (FORTRAN) procedure, see Chapter 4. in [An99]. This resulted in small changes in the mean R values. The procedure for constraints and for assembling the isotopic wings to the backbone along the stability line remained as described in [An04].
Acknowledgement
The author is indebted to Yury Kozhedub (St. Petersburg State University) for the helpful criticism regarding the evaluation of uranium charge radius data.
Remarks
1) For the neutron the <r2> value is given in fm2.
2) For the proton radius the Lamb shift and the constraint with the deuteron radius are also taken into account; see the references and data in the second paragraph of section 2.1 (p.187) of [An04].
3) For He and Li the OIS experimental technique is accompanied by recent high-precisity theoretical calculations, resulting in a practically new method of δR determination; see also the respective references.
4) For Eu, there are two reference nuclei: A0 = 145 and 151.
5) For Er, there are two reference nuclei: A0 = 150 and 166.
6) For Re, Po, Rn, Fr, Ra and Cm there are no
experimental R data. Reference radii R0
are calculated by the formula
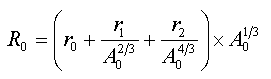
with the parameters: r0 = 0.9071(13) fm, r1 = 1.105(25) fm, r2 = ‑0.548(34) fm, which are the results of a least-squares fit to radii along the line of stability, see table 2. in [An04]. These parameters are not independent. Therefore, - to be on the safe side -, for the error the value 2×(ΔR0,ind) was used, where ΔR0,ind is the value calculated by the assumption of independent parameters.
References
| Hu61 Hull, R.J., and Stroke, H.H.: J. Opt. Soc. Am., 51 (1961) 1203 | Tl |
| Go69 Goorvitch, D., et al.: Phys. Rev., 188 (1969) 1897 | Tl |
| Fo82 Foot, C.J., et al.: Proc. Roy. Soc (L.), A384 (1982) 205 | Zn |
| Dy85 Dyer, P., et al.: Phys. Rev., C31 (1985) 240 | Sm |
| Al88b Alkhazov, G.D., et al.: LNPI Preprint No. 1417 (1988) 20 | Gd |
| Bo89 Borchers, W., et al.: Physics Letters, B216 (1989) 7 | |
| En90 England, J.G., et al.: J. Phys. G: Nucl. Part. Phys., 16 (1990) 105 | Sm |
| Sc91 Schulz, Ch., et al.: J. Phys. B.: At. Mol. Opt. Phys., 24 (1991) 4831 | Yb |
| Le92 Letokhov, V.S., et al.: Journ. Phys. G18 (1992) 1177 | (From Ba04) Eu, Sm, Nd |
| Li92 Lievens, P., et al.: Phys. Rev., C46 (1992) 797 | Sr |
| Li96 Lievens, P., et al.: Europhysics Letters, 33/1 (1996) 11 | Kr, Sr |
| Ve96 Vermeeren, L., et al.: Journ. Phys. G22 (1996) 1517 | Ca |
| El98 Elliott, S.R., et al.: Phys. Rev. C57 (1998) 583 | U |
| |
|
| An99 Angeli, I.: Table of Nuclear Root Mean Square Charge Radii, INDC(HUN)-033, Sept. 1999 | |
| (IAEA Nuclear Data Section, Vienna). Available also at <http://www.nds.iaea.or.at/indc-sel.html>. | |
| |
|
| An04 Angeli, I.: Atomic Data and Nuclear Data Tables, 87 (2004) 185 | (Table) |
| Ba04 Barzakh, A.E., et al.: Eur. Phys. J. A22 (2004) 69 | Eu |
| Ew04 Ewald, G., et al.: Phys. Rev. Letters, 93 (2004) 113002 | (See Ew05, Nö05a) Li |
| Ga04 Gangrsky, Yu.P., et al.: J. Phys. G: Nucl. Part. Phys., 30 (2004) 1089 | Ti |
| Wa04 Wang, L.-B., et al.: Phys. Rev. Letters, 93 (2004) 142501 | He |
| |
|
| Ba05 Barzakh, A.E., et al.: Phys. Rev., C72 (2005) 017301 | Gd |
| Dr05 Drake, G.W., et al.: Can. J. Phys., 83 (2005) 311 | He (Δ<r^2> in Mu07), Li |
| Ew05 Ewald, G., et al.: Phys. Rev. Letters, 94 (2004) 039901 | (Erratum to Ew05) Li |
| LB05 F.LeBlanc, et al.: Phys. Rev. C72 (2005) 034305 | Sn |
| Nö05 Nörtershäuser, W., et al.: Eur. Phys. J. A25 (2005) 199 | (See Nö05a) Li |
| Nö05a Nörtershäuser, W., et al.: Hyperfine Interactions, 162 (2005) 93 | Li |
| |
|
| Ga06 Gangrsky, Y. et al.: Hyperfine Interactions, 171 (2006) 209 | Sc |
| Mo06 Morton, D.C., et al.: Phys. Rev., A73 (2006) 034502 | He |
| Sá06 Sánchez, R., et al.: Phys. Rev. Letters, 96 (2006) 033002 | Li |
| Sá06a Sánchez, R., et al.: Hyperfine Interactions, 171 (2006) 181 | Li |
| Se06 Seliverstov, M., et al.: Hyperfine Interactions, 171 (2006) 225 | (results in DW07)Pb |
| Si06 Sifi, R., et al.: Hyperfine Interactions, 171 (2006) 173. | Te |
| Pu06 Puchalski, M., et al.: Phys. Rev. Letters, 97 (2006) 133001 | (Theor. eval. of Sá06, Ri94) Li |
| Ve06 Verney, D., et al.: Eur. Phys. J., A30 (2006) 489 | Ir |
| |
|
| Ch07 Cheal, B., et al.: Physics Letters, B645 (2007) 133 | Y |
| DW07 De Witte, H., et al.: Phys. Rev. Letters, 98 (2007) 112502 | Pb |
| Ko07 Kozhedub, Y.: Private communication (2007) | U |
| Li07 Libert, J., et al.: Nucl. Phys., A786 (2007) 47 | Te |
| Mu07 Mueller, P., et al.: Phys. Rev. Letters, 99 (2007) 252501 | He |
| Ro07 Roussière, B.: Private communication (2007) | Te |
| |
|
| Bl08 Blaum, K., et al.: Nucl. Phys., A799 (2008) 30 | Ar |
| Fe08 Fedorov, D.: Private communicaton (2008) | Gd |
| Ma08 Marinova, K.: Private communication (2008) | Ar, Sc |
| |
|
| |
CDFE Head: Vladimir V. Varlamov